$$\require{color}$$ $$\require{amsmath}$$ $$\require{cancel}$$ $$\definecolor{purple}{RGB}{226, 15, 233}$$ $$\definecolor{grey}{RGB}{177, 159, 149}$$ $$\newcommand{\ii}{\mathbf{i}}$$ $$\newcommand{\parll}{ {\mathbin{\parallel}} }$$ $$\newcommand{\prll}{{\mathbin{\!/\mkern-5mu/\!}}}$$

Topic 5 Applications of Integrals

5.1 Area between Curves

To find the area between curves, we identify a variable and use the differential in that variable as the width and the distance between the curve as the height and approximate the area using the Riemann sum of such a partition.

If the curves are given by \(y=f(x)\) and \(y=g(x)\) with \(a\le x\le b\), then the area between the curves may be set up as \[ \text{Area Between Curves}=\int_a^b|f(x)-g(x)|\mathrm{d}x \] Because the distance in \(y\) direction is easier to calculate.

If the curves are given by \(x=p(y)\) and \(x=q(y)\) with \(c\le y\le d\), then the area between the curves may be set up as \[ \text{Area Between Curves}=\int_c^d|p(y)-q(y)|\mathrm{d}y \] Because the distance in \(x\) direction is easier to calculate.

The absolute value sign can be removed by breaking the area into sub-areas.

Exercise 5.1 Sketch the graph of curves \(y=4-x^2\), \(y=2x+1\), \(x=-2\), and \(x=0\), and find the area enclosed by those curves.

Solution.

The graph of the curves shows that a vertical rectangular slice of the region has an area \([(4-x^2)-(2x+1)]\mathrm{d} x\).

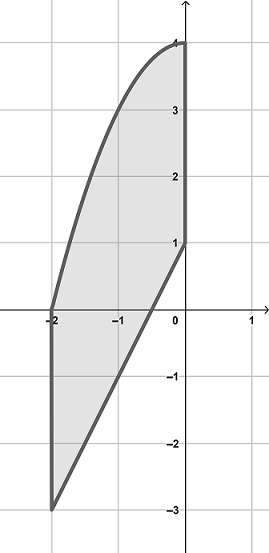
Area Between Two Curves

Then the area of the region can be calculated by the definite integral \[ \int_{-2}^0[(4-x^2)-(2x+1)]\mathrm{d} x=(-\frac{x^3}{3}-x^2+3x)|_{-2}^0=\frac{22}{3}. \]

Exercise 5.2 Sketch the graph of curves \(y=x^2-2\) and \(y=2\), and find the area enclosed by those curves.

Solution.

Solve the system of equations \[ \begin{cases} y=x^2-2\\ y=2, \end{cases} \] we get two intersection points \((-2, 2)\) and \((2, 2)\). Over the interval \([-2, 2]\), \(x^2-2\le 2\). Then the area of the region can be calculated by the definite integral \[ \int_{-2}^2[2-(x^2-2)]\mathrm{d} x=2\int_{0}^2(4-x^2)\mathrm{d} x =2(4x-\frac{x^3}{3})|_{0}^2=\frac{32}{3}. \]

Area Between Two Curves

Exercise 5.3 Sketch the graph of curves \(y=x^2+x-2\) and \(y=1-x\), and find the area enclosed by those curves.

Solution.

Solve the system of equations \[ \begin{cases} y=x^2+x-2\\ y=1-x, \end{cases} \] we get two intersection points \((-3, 4)\) and \((1, 0)\). Since the function \((x^2+x-2)\le (1-x)\) for \(-3\le x\le 1\), the area of the region can be calculated by the definite integral \[ \int_{-3}^1[(1-x)-(x^2+x-2)]\mathrm{d} x=(3x-\frac{x^2}{2}-\frac{x^3}{3})|_{-3}^1=\frac{32}{3}. \]

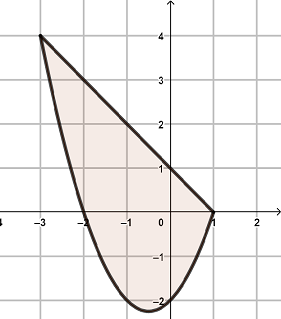
Area Between Two Curves

Exercise 5.4 Sketch the graph of curves \(y=\cos x\) and \(y=2\sin x\cos x\) with \(-\pi/2\le x\le \pi/2\) and find the area between those curves.

Solution.

Solve the system of equations \[ \begin{cases} y=\cos x\\ y=2\sin x\cos x, \end{cases} \] we get three intersection points \((-\pi/2, 0)\), \((\pi/6, \sqrt{3}/2)\) and \((\pi/2, 0)\). The graph of the functions are shown below.

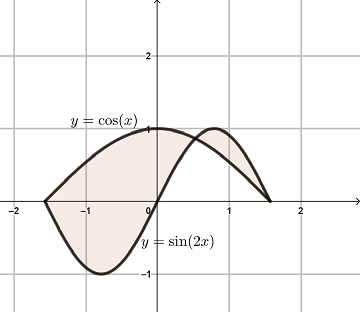
Area Between Two Curves

The area of the region can be calculated by the sum of two definite integral \[ \begin{aligned} &\int_{-\pi/2}^{\pi/2}|\cos x-2\sin x\cos x|\mathrm{d} x\\ =&\int_{-\pi/2}^{\pi/6}[\cos x-2\sin x\cos x]\mathrm{d} x+\int_{\pi/6}^{\pi/2}[2\sin x\cos x-\cos x]\mathrm{d} x\\ =&-\frac14(1-2\sin x)^2\big|_{-\pi/2}^{\pi/6}+\frac14(2\sin x-1)\big|_{\pi/6}^{\pi/2}\\ =&\frac94+\frac14\\ =&\frac52. \end{aligned} \]

Exercise 5.5 Sketch the graph of curves \(y=|x|\) and \(y=-x^2+2\) and find the area enclosed by those curves.

Solution.

Solve the system of equations \[ \begin{cases} y=|x|\\ y=-x^2+2, \end{cases} \] we get three intersection points \((-1, 1)\), and \((1, 1)\). The graph of the functions are shown below.

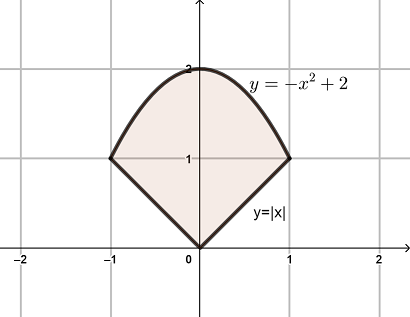
Area Between Two Curves

The area of the region can be calculated by the definite integral \[ \begin{aligned} &\int_{-1}^{1}||x|-(-x^2+2)|\mathrm{d} x\\ =&2\int_{0}^{1}||x|-(-x^2+2)|\mathrm{d} x\\ =&2\int_{0}^{1}(-x^2+2-x)\mathrm{d} x\\ =&2(-\frac{x^3}{3}-\frac{x^2}{2}+2x)\big|_0^1\\ =&\frac73. \end{aligned} \]

Exercise 5.6 Sketch the graph of curves \(x+y^2=5\) and \(y^2=x+3\) and find the area enclosed by those curves.

Solution.

Solve the system of equations \[ \begin{cases} x+y^2=5\\ y^2=x+3, \end{cases} \] we get three intersection points \((1, -2)\), and \((1, 2)\). The graph of the functions are shown below.

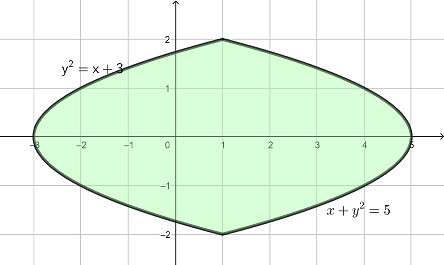
Area Between Two Curves

The area of the region can be calculated by the definite integral \[ \begin{aligned} &\int_{-2}^{2}|(5-y^2)-(y^2-3)|\mathrm{d} y\\ =&2\int_{0}^{2}(-2y^2+8)\mathrm{d} y\\ =&2(-\frac{2y^3}{3}+8y)\big|_0^2\\ =&\frac{64}{3}. \end{aligned} \]

Exercise 5.7 Sketch the graph of curves \(y=x\) and \(x=y^2-y-3\) and find the area enclosed by those curves.

Solution.

Solve the system of equations \[ \begin{cases} y=x\\ x=y^2-y-3, \end{cases} \] we get three intersection points \((-1, -1)\), and \((3, 3)\). The graph of the functions are shown below.

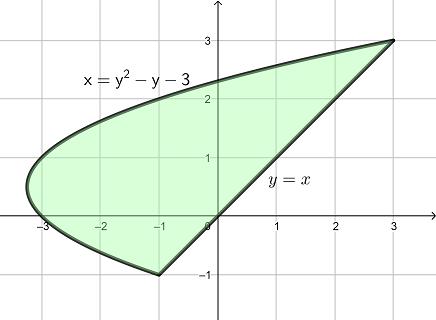
Area Between Two Curves

The area of the region can be calculated by the definite integral \[ \begin{aligned} &\int_{-1}^{3}|y-(y^2-y-3)|\mathrm{d} y\\ =&\int_{-1}^{3}(-y^2+2y+3)\mathrm{d} y\\ =&(-\frac{y^3}{3}+y^2+3y)\big|_{-1}^3\\ =&\frac{32}{3}. \end{aligned} \]

Exercise 5.8 Sketch the graph of curves \(x=y^4\) and \(y^2=2-x\) and find the area enclosed by those curves.

Solution.

Solve the system of equations \[ \begin{cases} x=y^4\\ y^2=2-x, \end{cases} \] we get three intersection points \((1, -1)\), and \((1, 1)\). The graph of the functions are shown below.

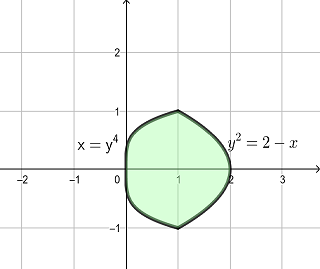
Area Between Two Curves

The area of the region can be calculated by the definite integral \[ \begin{aligned} &\int_{-1}^{1}|y^4-(2-y^2)|\mathrm{d} y\\ =&2\int_{0}^{1}(2-y^2-y^4)\mathrm{d} y\\ =&2(-\frac{y^5}{5}-\frac{y^3}{3}+2y)\big|_{0}^1\\ =&\frac{44}{15}. \end{aligned} \]

Exercise 5.9 Sketch the graph of curves \(y=x^2-1\) and \(y=x^3+x^2-x-1\) and find the area enclosed by those curves.

Solution.

Let \(D(x)=(x^2-1)-(x^3+x^2-x-1)=-x^3+x\). Solve \(D(x)=0\), we get three solutions \(x=-1\), \(x=0\), and \(x=1\). Using test point method or algebraic method, we find that \(D(x)<0\) for \(-1<x<0\) and \(D(x)>0\) for \(0<x<1\). The graph of the functions are shown below.

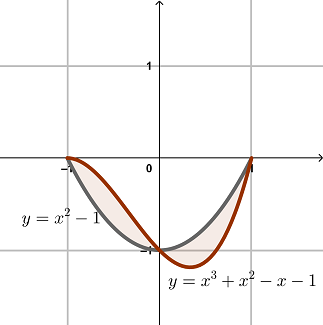
Area Between Two Curves

The area of the region can be calculated by the sum of two definite integral \[ \begin{aligned} &\int_{-1}^{1}|-x^3+x|\mathrm{d}x\\ =&2\int_{0}^{1}(-x^3+x)\mathrm{d} x =&2(-\frac{x^4}{4}+\frac{x^2}{2})\big|_{0}^1\\ =&\frac12. \end{aligned} \]

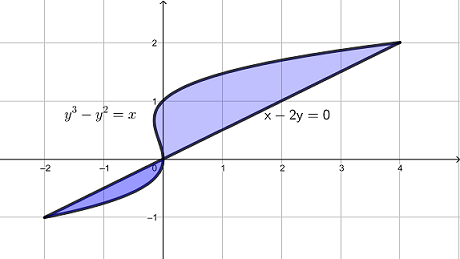
Exercise 5.10 Sketch the graph of curves \(x-2y=0\) and \(y^3-y^2=x\) and find the area enclosed by those curves.

Solution.

Since \(x\) is easier to solve, it is better to use the sum of areas horizontal rectangles, that is the area is given by \[ \int_a^b|x_R(y)-x_L(y)|\mathrm{d}y. \] Solve for \(x\) from the equations of the curves and set \(D(y)=(y^3-y^2)-2y=y^3-y^2-2y\). Solve \(D(y)=0\), we get three solutions \(y=-1\), \(y=0\), and \(y=2\). Using test point method or algebraic method, we find that \(D(y)>0\) for \(-1<y<0\) and \(D(y)<0\) for \(0<y<2\). The graph of the functions are shown below.

Area Between Two Curves

The area of the region can be calculated by the sum of two definite integral \[ \begin{aligned} &\int_{-1}^{2}|y^3-y^2-2y|\mathrm{d} y\\ =&\int_{-1}^{0}(y^3-y^2-2y)\mathrm{d} y-\int_{0}^{2}(y^3-y^2-2y)\mathrm{d} y\\ =&(\frac{y^4}{4}-\frac{x^3}{3}-y^2)\big|_{-1}^0-(\frac{y^4}{4}-\frac{x^3}{3}-y^2)\big|_{0}^2\\ =&\frac{5}{12}+\frac83\\ =&\frac{37}{12}. \end{aligned} \]