$$\require{color}$$ $$\require{amsmath}$$ $$\require{cancel}$$ $$\definecolor{purple}{RGB}{226, 15, 233}$$ $$\definecolor{grey}{RGB}{177, 159, 149}$$ $$\newcommand{\ii}{\mathbf{i}}$$ $$\newcommand{\parll}{ {\mathbin{\parallel}} }$$ $$\newcommand{\prll}{{\mathbin{\!/\mkern-5mu/\!}}}$$

Topic 4 Integrals

4.1 Areas and Distances

There are axiomatically and concrete ways to define area. In a concrete way, the unit square is defined to have area one and area of other shapes are defined by comparing with the unit square. To compute areas of complicated regions or surfaces, definite integral was developed. The idea is to subdivide a region into thin slices which can be approximately viewed as rectangles and then sum the areas of the rectangles as an approximation of the original region.

Definition 4.1 The area \(A\) of the region \(S\) that under the graph of a continuous function \(f\) on the interval \([a,b]\) is the limit of the area of approximating rectangles: \[ A=\lim_{n\to \infty}R_n=\lim_{n\to \infty}\Delta x\sum_{i=1}^nf(x_i^*), \] where \(\Delta x=\frac{b-a}{n}\) and \(x_i^*\) is a sample point in the subinterval \([a+(i-1)\Delta x, a+i\Delta x]\).

In the definition, the notation \(\sum\limits_{i=1}^nf(x_i^*)\), called the sigma notation, means taking the sum of \(f(x_i^*)\) for \(i\) from \(1\) to \(n\), i.e. \[ \sum\limits_{i=1}^nf(x_i^*)=f(x_1^*)+f(x_2^*)+\cdots+f(x_n^*). \]

For a continuous function \(f\), the sample points are often chosen to be the left, the right endpoints and the midpoint of the subintervals \([a+(i-1)\Delta x, a+i\Delta x]\).

If the sample points are chosen so that \(f(x_i^*)\) is the minimum (maximum) value of \(f\) on the \(i\)-th subinterval, then the sum is called the the lower sum (the upper sum, respectively).

When finding the area of a region using the definition, the following formulas will be useful. \[ \begin{aligned} \sum_{i=1}^n i=&\frac{n(n+1)}{2}\\[0.5em] \sum_{i=1}^n i^2=&\frac{n(n+1)(2n+1)}{6}\\[0.5em] \sum_{i=1}^n i^3=&\left[\frac{n(n+1)}{2}\right]^2\\[0.5em] \end{aligned} \]

Exercise 4.1 Use 3 rectangles to find each of the following types of estimate of the area under the graph of \(f=\sin x\) from \(x=0\) to \(x=\pi\).

1. \(L_3\) (sample points are left endpoints)
2. \(R_3\) (sample points are right endpoints)
3. \(M_3\) (sample points are midpoints)

Solution.

Divide the interval \([0, \pi]\) into three subintervals \([0,\frac{\pi}{3}]\), \([\frac{\pi}{3}, \frac{2\pi}{3}]\), \([\frac{2\pi}{3}, \pi]\). Then \[ L_3=\frac{\pi}{3}\left(\sin 0+\sin\frac{\pi}{3}+\sin\frac{2\pi}{3}\right)=\frac{\pi\sqrt{3}}{3}. \] \[ R_3=\frac{\pi}{3}\left(\sin\frac{\pi}{3}+\sin\frac{2\pi}{3}+\sin\pi\right)=\frac{\pi\sqrt{3}}{3}. \] \[ M_3=\frac{\pi}{3}\left(\sin\frac{\pi}{6}+\sin\frac{\pi}{2}+\sin\frac{5\pi}{6}\right)=\frac{2\pi}{3}. \]

Exercise 4.2 Evaluate the upper and lower sums for \(f(x)=x^2+1\) on \([-1, 1]\) with \(n=4\).

Solution.

Divide the interval \([-1, 1]\) into four subintervals \([-1,-\frac12]\), \([-\frac12,0]\), \([0,\frac12]\), \([\frac12,1]\). Because \(f(x)\) is decreasing for \(x<0\) and increasing for \(x>0\). Then the lower sum is \[ B_4=\frac12\left(f(-\frac12)+f(0)+f(0)+f(\frac12)\right)=\frac94. \] \[ U_3=\frac12\left(f(-1)+f(-\frac12)+f(-\frac12)+f(1)\right)=\frac{13}4. \]

Exercise 4.3 A car is speeding up. The speeds of a car recorded every five seconds within a 20 seconds interval are shown in the following table.

Time (s)	0	5	10	15	20
Velocity (m/s)	20	28	32	35	40

Find lower and upper estimates for the distance that the care traveled during these 20 seconds.

Solution.

As the car is speeding up, the lower estimate is given by \[ 5(20+28+32+35)=525 ~\text{m}. \] The upper estimate is \[ 5(28+32+35+40)=625 ~\text{m}. \]

Exercise 4.4 Evaluate the sum \[ \sum_{k=1}^{20}(2k+1). \]

Solution.

Using the identity \(\sum_{k=1}^n k=\frac{n(n+1)}{2}\), we get \[ \sum_{k=1}^{n}(2k+1)=2\sum_{k=1}^nk+\sum_{k=1}^n 1=n(n+1)+n=n(n+2). \]

Exercise 4.5 Write using sigma notation and evaluate the sum of the terms \((k-1)^2\) for \(k=1,2,…,100.\)

Solution.

The sum is \[ \sum_{k=1}^{100}(k-1)^2=\sum_{i=1}^{99}i^2=\frac{99(99+1)(2\cdot 99+1)}{6}=328350. \]

4.2 Definite Integrals

Definition 4.2 (Definition of a Definite Integral) Let \(f\) be a function defined for \(a\le x\le b\). Define \(\Delta x=\frac{b-a}{n}\) and \(x_i=a+i\Delta x\). Let \(x_i^*\) be any sample points in the subintervals \([x_{i-1}, x_i]\). The function \(f\) is called integrable on \([a, b]\) if the limit \[ \lim\limits_{n\to \infty}\sum_{i=1}^nf(x_i^*)\Delta x \] exists and given the same value for any choice of samples points.

For a integral function \(f\) on \([a, b]\), we denote the above limit as \[ \int_a^bf(x)\mathrm{d}x=\lim\limits_{n\to \infty}\sum_{i=1}^nf(x_i^*)\Delta x \] and call it the definite integral of \(f\) from \(a\) to \(b\).

The symbol \(\int\), introduced by Leibnize, is called the integral sign. In the integral notation \(\int_a^bf(x)\mathrm{d}x\), the expression \(f(x)\) is called the integrand; \(a\) and \(b\) are called the limits of integration; more precisely, \(a\) is called the lower limit and \(b\) is called the uppper limits; the symbol \(\mathrm{d}x\) is the differential which indicates the “direction” of the integration, the procedure of calculating the integral, is along the \(x\)-axis.

The sum \(\displaystyle R_n=\sum\limits_{i=1}^nf(x_i^*)\Delta x\) is called a Riemann sum.

Theorem 4.1 If the function \(f\) is continuous or has finitely many discontinuities on \([a, b]\), then \(f\) is integrable on \([a, b]\).

Theorem 4.2 If the function \(f\) is integrable on \([a, b]\), then \[ \int_a^bf(x)\mathrm{d}x=\lim\limits_{n\to \infty}\sum_{i=1}^nf(x_i)\Delta x, \] where \(\Delta x=\frac{b-a}{n}\) and \(x_i=a=i\Delta x\).

Any Riemann sum gives an approximation to an integral. The midpoint approximation as shown below is frequently used. \[ \text{Midpoint Approximation}=\int_a^bf(x)\mathrm{d} x\approx \sum_{i=1}^n f(\bar{x_i})\Delta x, \] where \(\Delta x=\frac{b-a}{2}\) and \(\bar{x_i}=a+(i-\frac12)\Delta x\) are the midpoints.

From the definition of the definite integral, we obtain the following basic properties of definite integrals.

Theorem 4.3 (Basic Properties of the Definite Integral) Let \(f\) and \(g\) are integrable functions. Then

1. \[\displaystyle \int_a^bf(x)\mathrm{d}x=-\int_b^af(x)\mathrm{d}x\]
2. \[\displaystyle \int_a^af(x)\mathrm{d}x=0\]
3. \[\displaystyle \int_a^b c\mathrm{d}x=c(a-b)\] for any constant number \(c\).
4. \[\displaystyle \int_a^b[cf(x)+dg(x)]\mathrm{d}x=c\int_b^af(x)\mathrm{d}x+dc\int_b^af(x)\mathrm{d}x,\] where \(c\) and \(d\) are any real numbers.

We also have the comparison properties of the definite integral.

Theorem 4.4 (Comparison Properties of the Definite Integral) If \(f(x)\ge g(x)\) for \(a\le x\le b\), then \[ \displaystyle \int_a^bf(x)\mathrm{d} x\ge \int_a^bfg(x)\mathrm{d} x. \]

In particular, if \(f(x)\ge 0\) on \([a, b]\), then \(\displaystyle \int_a^bf(x)\mathrm{d} x\ge 0\).

If \(m\le f(x)\le M\) on \([a, b]\), then \(\displaystyle m(b-a)\le \int_a^bf(x)\mathrm{d} x\le M(b-a)\).

Exercise 4.6 Express the following limits as integrals.

\(\displaystyle \lim\limits_{n\to \infty}\sum_{i=1}^n(2x^*_i+1)\Delta x\) over \([0,3]\).

Solution.

View \(\sum\) as \(\int\), \(\Delta x\) as \(\mathrm{d}x\), and \(2x_i^*+1\) as \(2x+1\), we get \[ \int_0^3(2x+1)\mathrm{d}x= \lim_{n\to \infty}\sum_{i=1}^n(2x^*_i+1)\Delta x \]

Exercise 4.7 Express the following limits as integrals.

\(\displaystyle \lim\limits_{n\to \infty}\sum_{i=1}^n\sin(x_i^*)\cos(x^*_i)\Delta x\) over \([0,\pi/2]\).

Solution.

The sum in the limit can be viewed as a Riemann sum of the function \(f(x)=\sin x\cos x\). The limit then can be expressed as the integral \[ \lim_{n\to \infty}\sum_{i=1}^n\sin(x_i^*)\cos(x^*_i)\Delta x=\int_0^{\pi/2}\sin x\cos x\mathrm{d}x. \]

Exercise 4.8 The graph of the function \(f\) is shown below. Find the integral \(\displaystyle \int_0^4f(x)\mathrm{d}x\).

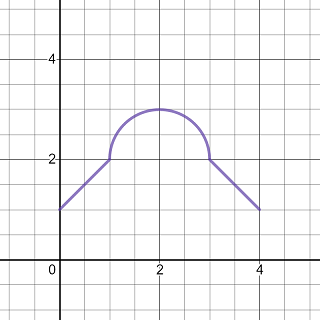
The graph of a function which looks like a cap

Solution.

The integral \(\int_0^4f(x)\mathrm{d}x\) computes the area under the graph. The area may be decomposed into a half disk a trapezoid, and a rectangle from top to bottom. The total area is \[ \frac12 \pi\cdot 1^2 + \frac12(2+4)\cdot 1+1\cdot4=7+\frac\pi2 \]

Exercise 4.9 Evaluate the integral using geometry and properties of integral. (Hint: Break down into several integrals of simpler functions.)

\(\displaystyle \int^1_0(2x+\sqrt{1-x^2})\mathrm{d} x\).

Solution.

The integral may be write as the sum of two integrals \[ \int^1_0(2x+\sqrt{1-x^2})\mathrm{d} x= \int^1_0 2x\mathrm{d} x +\int_0^1 \sqrt{1-x^2})\mathrm{d} x. \]

The region under the curve \(y=2x\) is a triangle whose area is \(\frac12\cdot 2\cdot 1=1\).

The region under the curve \(y=\sqrt{1-x^2}\) is a quarter of a disk whose area is \(\frac12\pi\cdot 1^2=\frac\pi4\).

Then \[ \int^1_0(2x+\sqrt{1-x^2})\mathrm{d} x= 1+\frac\pi4. \]

Exercise 4.10 Evaluate the integral using geometry and properties of integral. (Hint: Break down into several integrals of simpler functions.) \(\displaystyle \int^2_{-2}(\sqrt{4-x^2}-2|x|)\mathrm{d}x\).

Solution.

The integral may be write as the sum of two integrals \[ \int^2_{-2}(\sqrt{4-x^2}-2|x|)\mathrm{d}x=\int^2_{-2}\sqrt{4-x^2}\mathrm{d}x+2\int^2_{-2}|x|\mathrm{d}x. \]

The region under the curve \(y=\sqrt{4-x^2}\) is a half disk whose area is \(\frac12\pi\cdot 2^2=2\pi\).

The region under the curve \(y=|x|\) consists of two triangles with the same area \(\frac12\cdot 2\cdot 2=2\).

Then \[ \int^2_{-2}(\sqrt{4-x^2}-2|x|)\mathrm{d}x=2\pi-2\cdot2\cdot 2=2\pi-8. \]

Exercise 4.11 Evaluate the integral using the definition

\(\displaystyle \int^1_{0}(3x^2+1)\mathrm{d} x\).

Solution.

Since the function \(f(x)=3x^2+1\) is integrable, we may choose the samples points as the right endpoints. By the definition of Riemann sum, we have \[ \begin{aligned} \int^1_{0}(3x^2+1)\mathrm{d}x=&\lim_{n\to\infty}\left(\frac1n\sum_{i=1}^n\left(3\cdot\frac{i^2}{n^2}+1\right)\right)\\ =&\lim_{n\to\infty}\left(\left(\frac{3}{n^3}\sum_{i=1}^ni^2\right)+1\right)\\ =&\lim_{n\to\infty}\left(\frac{3}{n^3}\cdot\frac13n(n+1)(n+\frac12)\right)+1\\ =&2. \end{aligned} \]

Exercise 4.12 Evaluate the integral using the definition

\(\displaystyle \int^{1}_{2}(2x-3x^2)\mathrm{d} x\).

Solution.

Similar to the previous question, we have \[ \begin{aligned} &\int^{1}_{2}(2x-3x^2)\mathrm{d} x\\ =&\lim_{n\to\infty}\left(-\frac1n\sum_{i=1}^n\left(2\cdot\left(2-\frac in\right)-3\left(2-\frac{i}{n}\right)^2\right)\right)\\ =&\lim_{n\to\infty}\left(-\frac1n\sum_{i=1}^n\left(-8+10\frac in-3\frac{i^2}{n^2}\right)\right)\\ =&\lim_{n\to\infty}\left(8-\frac{10}{n^2}\sum_{i=1}^ni+\left(\frac{3}{n^3}\sum_{i=1}^ni^2\right)\right)\\ =&8-10\lim_{n\to\infty}\left(\frac{n(n+1)}{2n^2}\right)+3\lim_{n\to\infty}\left(\frac{n(n+1)(n+\frac12)}{3n^3} \right)\\ =&8-5+1=4. \end{aligned} \]

Exercise 4.13 Use the midpoint rule with the given \(n=3\) to approximate the following integral

\(\displaystyle \int^{\pi/2}_{-\pi/2}\cos x\mathrm{d} x\).

Solution.

By the midpoint rule, the integral is approximately \[ \int^{\pi/2}_{-\pi/2}\cos x\mathrm{d} x\approx \frac\pi3\left(\cos\left(-\frac\pi3\right)+\cos 0+\cos\left(\frac\pi3\right)\right)=\frac{2\pi}3. \]

Exercise 4.14 Evaluate the limit using a definite integral \(\displaystyle \lim\limits_{n\to\infty}\frac{3}{n}\sum_{i=1}^n\sqrt{1+\frac{3i}{n}}\).

Solution.

Take \(\Delta x=\frac3n\) and \(x_i=a+i\Delta x=a+\frac{3i}{n}\). If we take \(a=1\), then we get \(b=4\) from \(\Delta x=\frac{b-a}{n}=\frac3n\). Let \(f(x)=\sqrt{x}\). Then \[ \lim_{n\to\infty}\frac{3}{n}\sum_{i=1}^n\sqrt{1+\frac{3i}{n}}=\int_1^4\sqrt{x}\mathrm{d}x=\frac{14}{3} \]

Exercise 4.15 Find the maximum and minimum of the function \(f(x)=\frac{1}{x^2+1}\) over \([0, 2]\) and estimate the range of the value of the integral

\(\displaystyle \int^{-1}_{1}\frac{1}{x^2+1}\mathrm{d} x\).

Solution.

Since \(f'(x)=-\frac{2x}{(x^2+1)^2}<0\) for \(x>0\), the function is decreasing and hence the maximum is \(f(0)=1\) and the minimum is \(f(2)=\frac15\).

By the integral comparison theorem, \[ \frac25=\int^{-1}_{1}\frac15\mathrm{d} x\le \int^{-1}_{1}\frac{1}{x^2+1} \mathrm{d} x\le \int^{-1}_{1}1\mathrm{d} x=2 \]

4.3 Fundamental Theorem of Calculus

If \(f\) is a continuous function, apply the mean value theorem to the interval \([x, x+h]\) and let \(h\to 0\), we can obtain the following fundamental result in Calculus.

Theorem 4.5 (Fundamental Theorem of Calculus I) Let \(f\) be a continuous function on \([a, b]\). Then the function \[ g(x)=\int_a^xf(t)\mathrm{d}t\qquad a\le x\le b \] is continuous on \([a,b]\) and differential be on \((a, b)\) with the derivative \[ g'(x)=\frac{\mathrm{d}}{\mathrm{d}x}\int_a^xf(t)\mathrm{d}t=f(x). \]

Using the above theorem, to calculate an definite integral, we only need to find an antiderivative.

Theorem 4.6 (Fundamental Theorem of Calculus II) Let \(f\) be a continuous function on \([a, b]\). Then \[ \int_a^xf(x)\mathrm{d}x=F(b)-F(a), \] where \(F\) is an antiderivative of \(f\), that is, \(F'(x)=f(x)\).

Exercise 4.16 Find the derivative of the function \(f\) defined by the integral. \[ \displaystyle f(x)=\int^{1}_{x} \left(\frac12t^3-\frac43t-5\right)\mathrm{d} t. \]

Solution.

One way is to use properties of integrals and the FTC I. Another way is to use the FTC II. Here, we will use the FTC II.

Let \(F\) be a function such that \(F'(t)=\frac12t^3-\frac43t-5\). Then by the FTC II, \[f(x)=F(1)-F(x).\] Therefore, \[ f'(x)=-F'(x)=-\frac12x^3+\frac43x+5. \]

Exercise 4.17 Find the derivative of the function \(f\) defined by the integral. \[ \displaystyle f(x)=\int_{x}^0\frac{1}{t^2+t+1}\mathrm{d} t. \]

Solution.

Let \(F\) be a function such that \(F'(t)=\frac{1}{t^2+t+1}\). Then by the FTC II, \[f(x)=F(0)-F(x).\] Therefore, \[ f'(x)=-F'(x)=-\frac{1}{x^2+x+1}. \]

Exercise 4.18 Find the derivative of the function \(f\) defined by the integral. \[ \displaystyle f(x)=\int_{1}^{x^2}(1+\sin(t^2))\mathrm{d} t. \]

Solution.

Let \(F\) be a function such that \(F'(t)=1+\sin(t^2)\). Then by the FTC II, \[f(x)=F(x^2)-F(1).\] Therefore, by the chain rule, \[ f'(x)=F'(x^2)(x^2)'=2x(1+\sin(x^4)). \]

Exercise 4.19 Find the derivative of the function \(f\) defined by the integral. \[ \displaystyle f(x)=\int_{\sqrt{x}}^{x^2}\theta\cos\theta \mathrm{d} \theta. \]

Solution.

Let \(F\) be a function such that \(F'(\theta)=\theta\cos\theta\). Then by the FTC II, \[f(x)=F(x^2)-F(\sqrt{x}).\] Therefore, by the chain rule, \[ f'(x)=F'(x^2)(x^2)'-F'(\sqrt{x})(\sqrt{x})'=2x^3\cos(x^2)-\frac12\cos(\sqrt{x}). \]

Exercise 4.20 Evaluate the following integral. \[ \displaystyle \int_{-1}^{2}(4x^3-2x+1)\mathrm{d} x. \]

Solution.

We find an antiderivative first and then apply the FTC. \[ \begin{aligned} \int (4x^3-2x+1)\mathrm{d} x=&4\int x^3\mathrm{d}x-2 \int x\mathrm{d} x + \int 1\mathrm{d} x\\ =&4\frac{x^{3+1}}{3+1}-2\frac{x^{1+1}}{1+1}+x+C\\ =&x^4-x^2+x+C. \end{aligned} \] By the FTC, \[ \int_{-1}^{2}(4x^3-2x+1)\mathrm{d} x=(x^4-x^2+x)|_{-1}^2=15. \]

Exercise 4.21 Evaluate the following integral. \[ \displaystyle \int_{0}^{\pi/2}(2x+\cos x)\mathrm{d} x. \]

Solution.

We find an antiderivative first and then apply the FTC. \[ \begin{aligned} \int(2x+\cos x)\mathrm{d} x=&2\int x\mathrm{d} x+\int\cos x\mathrm{d} x\\ =&x^2+\sin x+C \end{aligned} \] By the FTC, \[ \int_{0}^{\pi/2}(2x+\cos x)\mathrm{d} x=(x^2+\sin x)|_{0}^{\pi/2}=\frac{\pi^2}{4}+1. \]

Exercise 4.22 Evaluate the following integral. \[ \displaystyle \int_{0}^{1}(x-1)^2\mathrm{d} x. \]

Solution.

We find an antiderivative first and then apply the FTC. \[ \begin{aligned} \int(x-1)^2\mathrm{d} x=&\int(x^2-2x+1)\mathrm{d} x\\ =&\frac{x^3}{3}-x^2+x+C \end{aligned} \] By the FTC, \[ \int_{0}^{1}(x-1)^2\mathrm{d} x=(\frac{x^3}{3}-x^2+x)|_{0}^{1}=\frac13. \]

Exercise 4.23 Evaluate the following integral. \[ \displaystyle \int_{1}^{4}\frac{x-1}{\sqrt{x}}\mathrm{d} x. \]

Solution.

We find an antiderivative first and then apply the FTC. \[ \begin{aligned} \int \frac{x-1}{\sqrt{x}} \mathrm{d} x=&\int(x^{\frac{1}{2}}-x^{-\frac12})\mathrm{d} x\\ =&\frac23x^{\frac32}-2x^{\frac12}+C \end{aligned} \] By the FTC, \[ \int_{1}^{4}\frac{x-1}{\sqrt{x}}\mathrm{d} x=(\frac23x^{\frac32}-2x^{\frac12})|_{1}^{4}=\frac83. \]

Exercise 4.24 Evaluate the following integral. \[ \displaystyle \int_{0}^{1}\left(\frac{x-1}{\sqrt{x}+1}+\frac{1}{\cos^2 x}\right)\mathrm{d} x. \]

Solution.

We find an antiderivative first and then apply the FTC. \[ \begin{aligned} \int \left(\frac{x-1}{\sqrt{x}+1}+\frac{1}{\cos^2 x}\right) \mathrm{d} x=&\int(\sqrt{x}-1+\sec^2x)\mathrm{d} x\\ =&\frac23x^{\frac32}-x+\tan x+C \end{aligned} \] By the FTC, \[ \int_{0}^{1}\left(\frac{x-1}{\sqrt{x}+1}+\frac{1}{\cos^2 x}\right)\mathrm{d} x=(\frac23x^{\frac32}-x+\tan x)|_{0}^{1}=\tan 1-\frac13. \]

Exercise 4.25 Evaluate the following integral. \[ \displaystyle \int_{0}^{4}|1-\sqrt{x}|\mathrm{d} x. \]

Solution.

Because the integrand involves the absolute value function, we need to rewrite it as a piecewise function without absolute value sign.

Because \(1-\sqrt{x}>0\) for \(0\le x<1\) and \(1-\sqrt{x}<0\) for \(x>1\). Then \[ |1-\sqrt{x}|=\begin{cases} 1-\sqrt{x} & 0\le x\le 1\\ \sqrt{x}-1 & 1<x \end{cases} \] and \[ \begin{aligned} \int_{0}^{4}|1-\sqrt{x}|\mathrm{d} x=&\int_{0}^{1}(1-\sqrt{x})\mathrm{d} x+\int_{1}^{4}(\sqrt{x}-1)\mathrm{d} x\\ =& (x-\frac23x^{\frac32})|_0^1+(\frac23x^{\frac32}-x)|_1^4\\ =& \frac13+\frac53=2. \end{aligned} \]

4.4 Indefinite Integrals

By the Fundamental Theorem of Calculus, when calculating a definite integral, we may first find an antiderivative. To be convenient, we use the notation \(\int f(x)\mathrm{d}x\) to denote the most general antiderivative of \(f\) and call it the indefinite integral of \(f\).

Let \(F\) be a differentiable function. The net change \(F(b)-F(a)\) equals the integral of the rate of change: \[ F(b)-F(a)=\int^b_aF'(x)dx \]

Exercise 4.26 Find the general indefinite integral.

\[ \displaystyle \int \sqrt[3]{x^2}\mathrm{d} x. \]

Solution.

\[ \int \sqrt[3]{x^2}\mathrm{d} x=\int x^{\frac23}\mathrm{d}x=\frac35x^{\frac53}+C. \]

Exercise 4.27 Find the general indefinite integral.

\[ \displaystyle \int (t+1)(t-2) \mathrm{d} t. \]

Solution.

\[ \int (t+1)(t-2) \mathrm{d} t=\int (t^2-t-2)\mathrm{d}t=\frac{t^3}{3}-\frac{t^2}{2}-2t+C. \]

Exercise 4.28 Find the general indefinite integral.

\[ \displaystyle \int \frac{1+\sqrt{u}}{\sqrt[3]{u}} \mathrm{d} u. \]

Solution.

\[ \int \frac{1+\sqrt{u}}{\sqrt[3]{u}} \mathrm{d} u=\int (u^{-\frac13}+u^{\frac12-\frac13}) \mathrm{d} u=\frac32u^{\frac23}+\frac67u^{\frac76}+C. \]

Exercise 4.29 Find the general indefinite integral.

\[ \displaystyle \int \frac{\cos^2\theta+\sin\theta}{\cos^2\theta} \mathrm{d} \theta. \]

Solution.

\[ \int \frac{\cos^2\theta+\sin\theta}{\cos^2\theta} \mathrm{d} \theta=\int(1+\tan\theta\sec\theta) \mathrm{d} \theta=\theta+\sec\theta+C. \]

Exercise 4.30 The velocity function (in meters per second) for a particle moving along a line is given by \[ v(t)=2t^2-t-3. \]

1. Find the displacement of the particle during the time period \(0 < t < 2\).
2. Find the distance traveled during the time period \(0 < t < 2\).

Solution.
The displacement is the difference between the positions. Denote by \(s(t)\) the position function, then the displacement is \[ \begin{aligned} s(2)-s(0)=&\int_0^2v(t)\mathrm{d} t\\ =& \int_0^2 (2t^2-t-3)\mathrm{d} t\\ =&(\frac23t^3-\frac12t^2-3t)|_0^2\\ =&-\frac{16}{3}. \end{aligned} \]

Denote by \(d(t)\) the distance function, then \[ \begin{aligned} d(2)-d(0)=&\int_0^2|v(t)|\mathrm{d} t\\ =& \int_0^2 |2t^2-t-3|\mathrm{d} t\\ =& \int_0^{\frac32} (-2t^2+t+3)\mathrm{d} t + \int_{\frac32}^2 (2t^2-t-3)\mathrm{d} t\\ =&(-\frac23t^3+\frac12t^2+3t)|_0^{\frac32}+(\frac23t^3-\frac12t^2-3t)|_{\frac32}^2\\ =&\frac{27}{8}+\frac{17}{24}=\frac{49}{12}. \end{aligned} \]

4.5 Substitution Method

From the Fundamental Theorem, we see that differentiation and integration are as inverse process to each other. If we reverse the rule of differentiation, we will get a method to integrate a function.

Theorem 4.7 (The Substitution Rule) If \(u=g(x)\) is a differentiable function whose range is an interval \(I\) and \(f\) is continuous on \(I\), then \[ \int f(g(x))g'(x)\mathrm{d}x=\int f(u)\mathrm{d}u. \]

For a definite integral, we also need to substitute limits of integration when applying the substitution rule.

Theorem 4.8 (The Substitution Rule for Definite Integral) If \(g'(x)\) is continuous on \([a, b]\) and \(f(x)\) is continuous on the range of \(u=g(x)\), \([g(a), g(b)]\), then \[ \int_a^bf(g(x))g'(x)\mathrm{d}x=\int_{g(a)}^{g(b)}f(u)\mathrm{d}u. \]

Applying the chain rule to functions with symmetries will simplify the calculation.

Proposition 4.1 Suppose that \(f\) is a continuous function on \([-a, a]\).

1. If \(f\) is an odd function, that is \(f(-x)=-f(x)\), then \[\displaystyle \int_{-a}^af(x)\mathrm{d}x =0.\]
2. If \(f\) is an even function, that is \(f(-x)=f(x)\), then \[\displaystyle \int_{-a}^af(x)\mathrm{d}x =2\int_0^af(x)\mathrm{d}x.\]

Exercise 4.31 Evaluate the following integral. \[ \displaystyle \int x\sqrt{x^2+1}\mathrm{d} x. \]

Solution.

Let \(u=x^2+1\). Then \(\mathrm{d}x=\frac{\mathrm{d}u}{2x}\) and \[ \begin{aligned} \int x\sqrt{x^2+1}\mathrm{d}x=&\int x\sqrt{u}\frac{\mathrm{d}u}{2x}\\ =& \frac12\int\sqrt{u} \mathrm{d}u\\ =&\frac12\frac23u^{\frac32}+C\\ =&\frac13(x^2+1)^{\frac32}+C \end{aligned} \]

Note: You may also try the substitution \(u=\sqrt{x^2+1}\).

Exercise 4.32 Evaluate the following integral. \[ \displaystyle \int \frac{x^2}{\sqrt{1-x^3}}\mathrm{d} x. \]

Solution.

One way is to let \(u=1-x^x\).

Here, I would like to show you another way. Let \(u=\sqrt{1-x^3}\). Then \(u^2=1-x^3\) and \(\mathrm{d}x=\frac{2u\mathrm{d}u}{-3x^2}\). Therefore, \[ \begin{aligned} \int \frac{x^2}{\sqrt{1-x^3}}\mathrm{d} x=&\int \frac{x^2}{u}\frac{2u\mathrm{d}u}{-3x^2}\\ =& -\frac23\int \mathrm{d}u\\ =&-\frac23u+C\\ =&-\frac23\sqrt{1-x^3}+C \end{aligned} \]

Exercise 4.33 Evaluate the following integral. \[ \displaystyle \int(\sin\theta\cos^2\theta)\mathrm{d} \theta. \]

Solution.

Let \(u=\cos\theta\). Then \(\mathrm{d}\theta=\frac{\mathrm{d}u}{-\sin theta}\). Therefore, \[ \begin{aligned} \int (\sin\theta\cos^2\theta)\mathrm{d} \theta=&\int((\sin\theta) u^2) \frac{\mathrm{d}u}{-\sin \theta}\\ =& -\int u^2 \mathrm{d}u\\ =&-\frac13u^3+C\\ =&-\frac13\cos^2\theta+C \end{aligned} \]

Exercise 4.34 Evaluate the following integral. \[ \displaystyle \int\sec^2 t\tan t\mathrm{d} t. \]

Solution.

Let \(u=\tan t\). Then \(\mathrm{d}t=\frac{\mathrm{d}u}{\sec^2t}\). Therefore, \[ \begin{aligned} \int\sec^2 t\tan t\mathrm{d} t=&\int u\mathrm{d}u\\ =&\frac12u^2+C\\ =&\frac12\tan^2t+C \end{aligned} \]

Exercise 4.35 Evaluate the following integral. \[ \displaystyle \int \sqrt[3]{2x+1} \mathrm{d} x. \]

Solution.

You may simply let \(u=2x+1\).

Here, we let \(u=\sqrt[3]{2x+1}\). Then \(u^3=2x+1\) and \(\mathrm{d}x=\frac{3u^2\mathrm{d}u}{2}\). Therefore, \[ \begin{aligned} \int \sqrt[3]{2x+1} \mathrm{d} x=&\int u\frac{3u^2\mathrm{d}u}{2}\\ =&\frac32\int u^3\mathrm{d}u\\ =&\frac38u^4+C\\ =&\frac38(\sqrt[3]{2x+1})^4+C \end{aligned} \]

Exercise 4.36 Evaluate the following integral. \[ \displaystyle \int (3x-2)^5 \mathrm{d} t. \]

Solution.

One way is to use the binomial formula the expand the integrand and then integrate.

Here we use a substitution to make the calculation easier.

Let \(u=3x-2\). Then \(\mathrm{d}x=\frac{\mathrm{d}u}{3}\). Therefore, \[ \begin{aligned} \int (3x-2)^5 \mathrm{d} t=&\int u^5\frac{\mathrm{d}u}{3}\\ =&\frac13\int u^5\mathrm{d}u\\ =&\frac1{18}u^6+C\\ =&\frac1{18}(3x-2)^6+C \end{aligned} \]

Exercise 4.37 Evaluate the following integral. \[ \displaystyle \int_1^4 \frac{\sin(\sqrt{x})}{\sqrt{x}}\mathrm{d} x. \]

Solution.

Let \(u=\sqrt{x}\). Then \(\mathrm{d}x=2\sqrt{x}\mathrm{d}u\) and \[ \frac{\sin(\sqrt{x})}{\sqrt{x}}\mathrm{d} x=2\sin(u)\mathrm{d}u. \] Therefore, \[ \begin{aligned} \int_1^4 \frac{\sin(\sqrt{x})}{\sqrt{x}}\mathrm{d} x =&\int_{u(1)}^{u(4)} 2\sin u\mathrm{d} u\\ =&2\int_1^2\sin u\mathrm{d}u\\ =&-2\cos u|_1^2=-2(\cos 2-\cos 1). \end{aligned} \]

Note: To avoid the mistake of forgetting substitute the integral limits, it will be better to find the indefinite integral first.

Exercise 4.38 Evaluate the following integral. \[ \displaystyle \int_1^2 \frac{\cos(\pi/x^2)}{x^3}\mathrm{d} x. \]

Solution.

Let \(u=\frac{\pi}{x^2}\). Then \(\mathrm{d}x=\frac{x^3}{-2\pi}\mathrm{d}u\) and \[ \frac{\cos(\pi/x^2)}{x^3}\mathrm{d} x=\frac{\cos u}{-2\pi}\mathrm{d}u. \] Therefore, \[ \begin{aligned} \int_1^2 \frac{\cos(\pi/x^2)}{x^3}\mathrm{d} x =&\int_{u(1)}^{u(2)}\frac{\cos u}{-2\pi}\mathrm{d}u\\ =&\frac1{-2\pi} \int_{\pi}^{\pi/4}\cos u\mathrm{d}u\\ =&\frac1{-2\pi}\sin u|_{\pi}^{\pi/4}=-\frac{\sqrt2}{4\pi}. \end{aligned} \]

Exercise 4.39 Evaluate the following integral. \[ \displaystyle \int_0^{\pi/4} \sin(2\theta)\cos(2\theta)\mathrm{d} \theta. \]

Solution.

There are different ways to find this integral.

One way is to let \(u=\sin(2\theta)\). Then \(\mathrm{d} u=2\cos(2\theta)\mathrm{d}\theta\) and \[ \sin(2\theta)\cos(2\theta)\mathrm{d} \theta=\frac12u\mathrm{d}u \] Therefore, \[ \begin{aligned} \int_0^{\pi/4} \sin(2\theta)\cos(2\theta)\mathrm{d} \theta =&\int_{u(0)}^{u(\pi/4)}\frac12u\mathrm{d}u\\ =&\frac12 \int_{0}^{1} u\mathrm{d}u\\ =&\frac14 u^2|_{0}^{1}=\frac14. \end{aligned} \]

Exercise 4.40 Evaluate the following integral. \[ \displaystyle \int_{-2}^{2}(x^3+x\sec^2x)\mathrm{d} x. \]

Solution.

Note that the function \(f(x)=x^3+x\sec^2x\) is an odd function, that is \(f(-x)=-f(x)\). If we let \(u=-x\),then \(\mathrm{d}x=-\mathrm{d}u\) and
\[ \begin{aligned} \int_{-2}^{2}(x^3+x\sec^2x)\mathrm{d} x=&-\int_{2}^{-2}((-u)^3+(-u)\sec^2(-u))\mathrm{d} u\\ =&-\int_{-2}^{2}(u^3+u\sec^2u)\mathrm{d} u\\ =&-\int_{-2}^{2}(x^3+x\sec^2x)\mathrm{d} x \end{aligned} \] Add to both sides the definite integral, we get \[ 2\int_{-2}^{2}(x^3+x\sec^2x)\mathrm{d} x=0. \] Therefore, \[ \int_{-2}^{2}(x^3+x\sec^2x)\mathrm{d} x=0. \]